あなたの脳も騙されている「モンティ・ホール問題」編

人間は錯覚する動物です。それは普段「簡単にわかっている」と考えている確率の問題においても、錯覚はおきます。

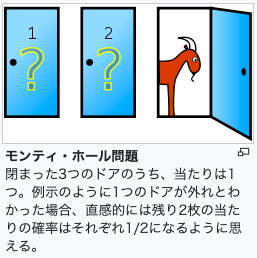
「モンティ・ホール問題」というのを知っていますか？これの問題は、モンティ・ホールという司会者を務めるアメリカのゲームショーの番組、「Let’s make a deal」の中で行われたゲームに関する論争に由来する名前です。

1990年9月9日発行、ニュース雑誌「Parade」にてマリリン・ボス・サヴァントが連載するコラム「マリリンにおまかせ」で、（投稿者が）クイズを出しました。

クイズの内容
答えをめぐっての騒動
正解はドアを変える
ゲームのルールを振り返る
錯覚を破る方法

クイズの内容

・あなたの前に閉じた3つのドアがあって、1つのドアの後ろには景品の自動車が、2つのドアの後ろには、はずれを意味するヤギがいる。

・あなたは自動車のドアを当てると自動車がもらえる。

・あなたが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。

・ここであなたは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。

あなたは（自動車をもらえる確率を高めるために）ドアを変更すべきだろうか？

マリリンは、「正解は『ドアを変更するだ』」と回答しました。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と説明したのです。

すると直後から、読者からの「彼女の解答は間違っている」との約1万通の投書がが殺到し、本問題は大議論に発展してしまいました。どうしてそうなったのか？

答えをめぐっての騒動

投書の中には、1000人近い博士号保持者からのものも含まれていた。その大部分は「ドアを変えても確率は五分五分（2分の1）であり、3分の2にはならない」とするものであった。中には過激な反対意見もあった。

あなたも、残りの2つのドアに自動車が隠されている確率は半々、1/2だからドアを変えても変えなくても結果は同じだと思うかもしれない。

これに対しマリリンは、より簡易にした表を掲載「ドアを変えれば勝てるのは3回の内2回、負けるのは3回の内1回だけ、しかしドアを変えなければ勝てるのは3回の内1回だけ」と述べました。

正解はドアを変える

侃侃諤々（かんかんがくがく）の議論の末、プロの数学者がコンピューターまで使った実験でマリリンの説明が正解だったことが証明されました。

さらに、「アメリカン・スタティスティシャン」「アメリカン・マスマティカル・マンスリー」「マスマティカル・サイエンティスト」「マスマティクス・ティーチャー」「ニューヨークタイムズ」等の媒体で細部まで議論され、その結果、マリリンの解答は基本的に正しいとされた。

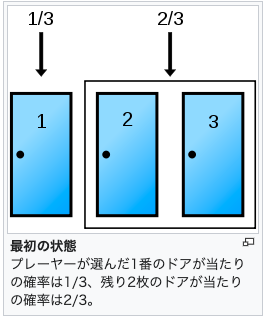
・もしあなたが最初に自動車のあるドアを選んでいたらその確率は3分の1で、残りの扉にヤギがいる。もしあなたが、最初にヤギのいるドアを選んだとしたのなら確率は3分の2で、残りの扉に自動車がある。

つまり、あたなの最初の選択は自動車よりヤギの可能性の方が高く、残りの2つのドアのどちらかに自動車があるのは確かなのだから、あなたは選択を変えた方が有利なのです。

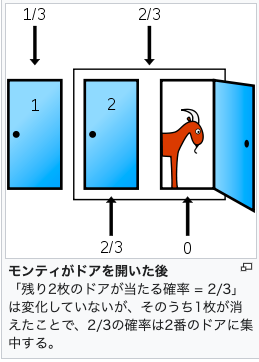
このモンティ・ホール問題の「問題」は、最初にドアを選んだ時点では自動車が当たる確率は完全に3分の1。しかし、そのあと司会者のモンティが残りの2つのドアからヤギのいる扉を1つ除外するために起こります。

この問題の本当の問題は、1万通の反論の投書が寄せられたように、本能的にマリリンの答えが間違っていると感じる点にあるのです。

あなたが最初のドアを選んだ後に、モンティがヤギのいるドアを必ず開くという行為が意味するものがすっぽりと抜け落ちてしまったところにあります。

ゲームのルールを振り返る

(1) 3つのドア (A, B, C) に（景品、ヤギ、ヤギ）がランダムに入っている。
(2) プレーヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。

このうち (3) と (4) の条件が重要で、もし (3) が決められていなければ（例えば開けるかどうかモンティが決められる）なら、このゲームはプレーヤーとモンティの心理戦であり、確率の問題ではなくなる。

また、(4) の条件次第では答えが逆になったり、答えを定めることができなくなる。つまり、モンティが景品を出してしまう可能性があるなら、問題の大前提が変わってしまう。

この(3)、(4)を頭に入れておかないと錯覚に陥り、必ず3つの扉のうちの1つにヤギがいる=1/3の確率だと、脳が解釈してしまうのです。